resistors in parallel ?

[littlejohn]

I need a 1.5 k 2watt resistor , can I use 2 1 watt resistors in parallel for testing purposes while waiting for a 2 watt to arrive?

[sam_sam_sam]

Re: resistors in parallel ?

You can use two 3k ohm resistor @ 1 watt in parallel to get 1.5k @ 2 watt that you are looking for

[eccerr0r]

Re: resistors in parallel ?

And two 750Ω 1W resistors in series would also result in a 1.5KΩ 2W resistance.

[sam_sam_sam]

Re: resistors in parallel ?

And two 750Ω 1W resistors in series would also result in a 1.5KΩ 2W resistance.

Are you sure about this because I thought that if one was 1 watt total because it would just add more resistance but I could be wrong

[eccerr0r]

Re: resistors in parallel ?

Do the math.

BTW, should always do the math. You can even do funny things with nonmatching resistors but yeah it gets complicated when they don't match as the power dissipated will be different if resistances are different.

[redwire]

Re: resistors in parallel ?

The heat to be dissipated would be shared over two parts, each one dissipates a ratio of the value a single part would. Regardless of whether the two are in series or parallel.
50-50 split so 1W each using two 750Ω series or 3kΩ parts parallel.
If you used a 2.2kΩ and 4.7kΩ in parallel, each see about 1.36W and 0.64W - the same ratio as their resistances.

[eccerr0r]

Re: resistors in parallel ?

Then you'll need a 1.5W 2k2 resistor which rounds up to 2W, and why not buy a 3k 2W resistor to begin with
With dissimilar resistors, probably only for last resort or if you have other values to burn... I was trying to do this with a 10R 2W and a 40R 10W in series for a 50R load, now need to calculate the system max sustained wattage... Then realize that inductance in the pair was too high for VHF frequencies...

[EasyGoing1]

Re: resistors in parallel ?

Do the math.

BTW, should always do the math. You can even do funny things with nonmatching resistors but yeah it gets complicated when they don't match as the power dissipated will be different if resistances are different.

Here's the math if anyone is interested or ever will be interested ...



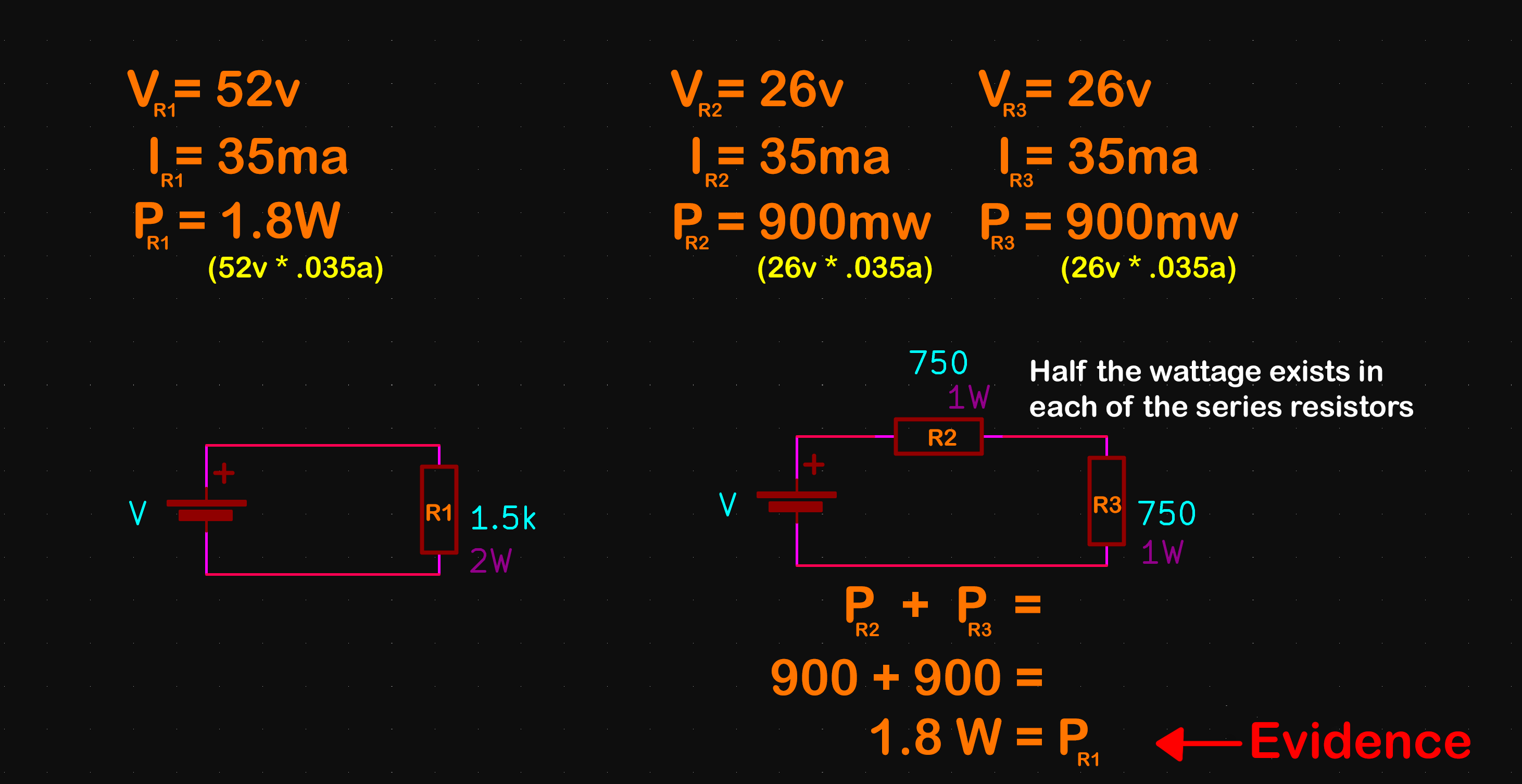
What I find particularly interesting about this thought exercise, is that like sam, my knee-jerk reaction to the statement was to pause and question it. And I think that is because we are used to thinking about net values - where resistors are concerned anyways - differently depending on whether the resistors are in series or parallel ... so I think naturally the brain wants to continue that pattern of thought even if the value in question is wattage dissipation. Which as it turns out, does not care if the resistors are in series or parallel, wattage dissipation adds up linearly.

[eccerr0r]

Re: resistors in parallel ?

I think the main reason to answer the way sam did is he was thinking about batteries and considering amps and not watts.

two 12V 1Ah batteries in series will give you 24V but still only 1Ah.

Now the rhetorical question: if you change the question to two 12V 1Wh batteries in series, how many watt hours do you get out of the system?

[sam_sam_sam]

Re: resistors in parallel ?

I think the main reason to answer the way sam did is he was thinking about batteries and considering amps and not watts.

two 12V 1Ah batteries in series will give you 24V but still only 1Ah

This is what I was thinking about but after I saw the math that EasyGoing did it cleared up the confusion about this thanks to both of you

[sam_sam_sam]

Re: resistors in parallel ?

Now the rhetorical question: if you change the question to two 12V 1Wh batteries in series, how many watt hours do you get out of the system?

I will run this test and give you a definite answer to this question over the weekend by doing an actual test I think I know the answer to this question but I want to know for sure that I am right because I have a way to do this test

[redwire]

Re: resistors in parallel ?

It's the difference between power and energy. Resistors are only concerned with power they dissipate, regardless of the time, how long they've been doing it.
Batteries are limited - if each battery has X watt-hours of energy, then two batteries gives you... well 2X. The energy available just adds up.

[petehall347]

Re: resistors in parallel ?

Batteries are limited - if each battery has X watt-hours of energy, then two batteries gives you... well 2X. The energy available just adds up.

only if in parallel . otherwise its the same as the lowest value .
resistors in series are the wattage of the lowest wattage one .
example .. 2 watts and 1 watts in series = 1 watt .

[redwire]

Re: resistors in parallel ?

In parallel you get double the Ah, in series you get double the voltage. So two batteries will always give the energy of... well... two batteries. Not one.
Where is the confusion on this I wonder.

[eccerr0r]

Re: resistors in parallel ?

in this case power and energy don't really matter, just take a fixed amount of time and the math works out.

This confusion is because some people equate amps (or amp hours) with, or as a proxy for watts (or watt hours), and then extrapolate to resistors, leading to improper conclusions.

[EasyGoing1]

Re: resistors in parallel ?

only if in parallel . otherwise its the same as the lowest value .
resistors in series are the wattage of the lowest wattage one .
example .. 2 watts and 1 watts in series = 1 watt .

I can't help but notice that this is similar to capacitors ... parallel ADDS values and series become some ratio of the total ... though this makes sense since a battery is just a pre-charged capacitor I suppose ... mathematically speaking ... or at least in some loose way they are.

[EasyGoing1]

Re: resistors in parallel ?

in this case power and energy don't really matter, just take a fixed amount of time and the math works out.

This confusion is because some people equate amps (or amp hours) with, or as a proxy for watts (or watt hours), and then extrapolate to resistors, leading to improper conclusions.

I struggle with these MAh ratings on these batteries ... so for example, a battery is rated at being capable of sustaining 3,000 MAh ... which says to me that it can continuously provide 3 amps for an hour ... but that never seems to be the observed reality ... in any specific case from what I remember back when I was trying to make sense of all that stuff.

I wanted to make an arduino based LiIon charger at one point and I specifically remember struggling with the actual HOW in calculating how many MAh were going into the battery as it charged.

[brownharris561]

Re: resistors in parallel ?

Here's the math if anyone is interested or ever will be interested ...



What I find particularly interesting about this thought exercise, is that like sam, my knee-jerk reaction to the statement was to pause and question it. And I think that is because we are used to thinking about net values - where resistors are concerned anyways - differently depending on whether the resistors are in series or parallel ... so I think naturally the brain wants to continue that pattern of thought even if the value in question is wattage dissipation. Which as it turns out, does not care if the resistors are in series or parallel, wattage dissipation adds up linearly.

Nice Explained!

[eccerr0r]

Re: resistors in parallel ?

only if in parallel . otherwise its the same as the lowest value .
resistors in series are the wattage of the lowest wattage one .
example .. 2 watts and 1 watts in series = 1 watt .

I can't help but notice that this is similar to capacitors ... parallel ADDS values and series become some ratio of the total ... though this makes sense since a battery is just a pre-charged capacitor I suppose ... mathematically speaking ... or at least in some loose way they are.

Not sure why or perhaps I forgot to, but to make it crystal clear, these conclusions are using the watt and amp confusion alluded to earlier, leading to unexpected and improper solutions.

While as rule of thumb using "lowest wattage" = "system wattage" works to be safe, it's more nuanced and potentially significantly pessimistic. You have to calculate dissipation individually to know system dissipation. For that example of the 50 ohm dummy load that I created with those 40 ohm 10W and 10 ohm 2W resistors. What is the system power limit? In this case it would actually be 10 watts if my math is right.

Now for batteries this is a problem because we have to deal with dead batteries. Dead batteries cause problems when in series, so yes, if you have a 120Wh battery in series with a 12Wh battery, you end up with some unknown watt hour system capacity that can't be computed without also knowing each battery's voltage and their characteristics, acceptable or not, when dead. If the battery voltages were both 12V then system power capability would be at least 24Wh; more if you can deal with consequences.

So yes there is a kind of geometric mean when dealing with series devices. Calculating it requires some care as well as understanding the consequences of such. This also includes the series capacitor issue.

I struggle with these MAh ratings on these batteries ... so for example, a battery is rated at being capable of sustaining 3,000 MAh ... which says to me that it can continuously provide 3 amps for an hour ... but that never seems to be the observed reality ... in any specific case from what I remember back when I was trying to make sense of all that stuff.

I wanted to make an arduino based LiIon charger at one point and I specifically remember struggling with the actual HOW in calculating how many MAh were going into the battery as it charged.

Most of the times the mAh ratings are due to "marketing exaggeration" if not for internal resistance issues. What you found is what you found (and correct for your situation), and the number printed is simply ... wrong.